Having grown up with Mathematica as my first programming language, it is only natural that I should want to tinker with the system now. Unfortunately, it is a proprietary system kept under the lock and key of WRI. The obvious solution to this problem is to program it again from the ground up. While I would have used assembly language in the past for this endeavour, we can get things done a lot faster with C++, though not without some serious systemic performance problems in some corner cases.

Naming things is hard. It is clearly some kind of Computer Algebra System. And, The Linux Edition was the first to be written, so it got called casl and then castle.

features of castle
some internal design decisions
exceptional control flow
C++ rant
asmcastle
pattern matching
compiler
screenshots

Features

Dependencies and external sources of code:

This first point is important because these C libraries are not exception safe, and I would like the ability to safely abort a long running calculation. This last point is noticable on low resolution displays: If the pixels of these images line up with the pixels of your display device and you have an RGB format, then one of these images should appear crisper than the other. If not, then the one that is supposed to be crisper will just look like the TikTok logo.


And a pure text comparison:


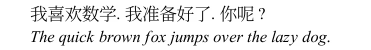
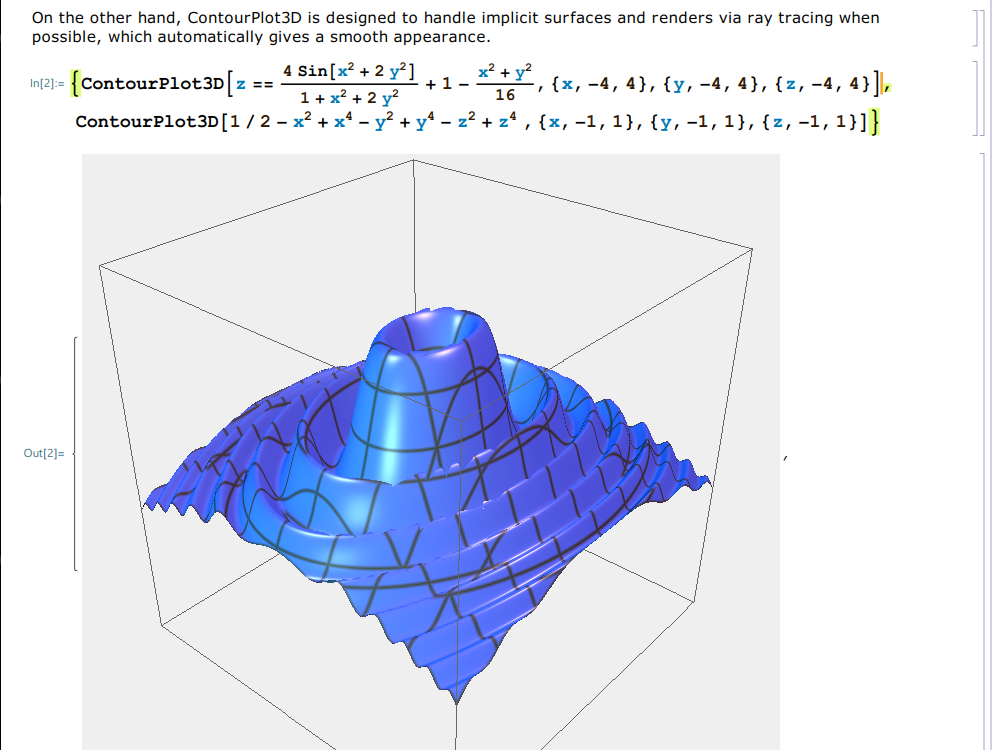
Other features completely implemented from scratch:

Internal use: pass a copy? or not?

Castle uses two raw pointer types ex and er for expressions. These are of course wrapped in higher level classes with automatic memory management and destructors, but the raw pointer types are used to pass and receive expressions through the function call boundary. Why deal with these raw pointers? Well, the C++ ABI for passing around, for example, classes such as unique_ptr is well-known to be terrible.

Dealing with raw pointers immediately brings up the question: does the caller own it (er)? or is the callee expected to take ownership (ex)? Leaving only one pointer type for both is common in programming, but forces a huge burden on the programmer as this kind of code is not self-documenting.

These two separate pointer types come with a huge caveat: the pointer aliasing rules of C. It is possible for a er and an ex to point to the same memory location, but the compiler is allowed to assume this is not the case. This can and does cause real bugs. Therefore castle comes with a configuration switch which either makes er and ex distinct types or the same type. In case of the former we can get checking at compile time of the eternal question "Was I supposed to pass a copy?", but the resulting binary is either invalid or cannot be produced with optimizations enabled. In the latter case, we can enable optimizations. Hence, the er / ex dichotomy is a debugging tool.

A typical function that uses expressions and passes them along looks like 

    void eparser::handle_ex(ex E)
    {
        uex e(E);
        handle_char(CHAR_NONE);
        if (error) {return;}
        handle_token_ex(e.release());
        e.kill_dead();
    }
The uex class is essentially a unique_ptr and is supposed to own a raw pointer that can either be null or a real expression. 
    struct uex {
        ex data;
        uex(): data(nullptr) {}
        uex(ex d): data(d) {}
        uex (const uex & other): data(ecopy(other.data)) {}
        ~uex() {if (data != nullptr) eclear(data);}
        ex release() {
            ex datacopy = data;
            data = nullptr;
            return datacopy;
        }
        ...
    }
Then, what is going on with kill_dead? Well, besides not having destructive moves in C++, the C++ compiler is not able to figure out that e.data == null at the end of this function, and hence emits the full code for ~uex()! That is, without the e.kill_dead(); and with g++ -O3, we get the code 
00000000000fcd40 <_ZN7eparser9handle_exEP9ex_struct>:
   fcd40:	endbr64 
   fcd44:	push   rbp
   fcd45:	mov    rbp,rdi
   fcd48:	sub    rsp,0x10
   fcd4c:	mov    QWORD PTR [rsp+0x8],rsi  ; constructor for uex
   fcd51:	mov    esi,0xffffffff
   fcd56:	call   10b970 <_ZN7eparser11handle_charEi>
   fcd5b:	mov    eax,DWORD PTR [rbp+0x1c8]
   fcd61:	mov    rsi,QWORD PTR [rsp+0x8]
   fcd66:	test   eax,eax
   fcd68:	jne    fcda0 <_ZN7eparser9handle_exEP9ex_struct+0x60>
   fcd6a:	mov    rdi,rbp
   fcd6d:	mov    QWORD PTR [rsp+0x8],0x0  ; put 0x0 in there for the release
   fcd76:	call   fbcb0 <_ZN7eparser15handle_token_exEP9ex_struct>
   fcd7b:	mov    rdi,QWORD PTR [rsp+0x8]  ; you dummy!
   fcd80:	test   rdi,rdi                  ; you just put 0x0 in there!
   fcd83:	je     fcd96 <_ZN7eparser9handle_exEP9ex_struct+0x56>
   fcd85:	mov    rax,QWORD PTR [rdi]
   fcd88:	sub    rax,0x10
   fcd8c:	mov    QWORD PTR [rdi],rax
   fcd8f:	jae    fcd96 <_ZN7eparser9handle_exEP9ex_struct+0x56>
   fcd91:	call   125480 <_Z12ex_cleardoneP9ex_struct>
   fcd96:	add    rsp,0x10
   fcd9a:	pop    rbp
   fcd9b:	ret 
    ...
Therefore, the code for kill_dead is 
    struct uex {
        ...
        void kill_dead() {
            assert(data == nullptr);
            data = nullptr;
        }
        ...
    }
and can be used at any time to stop gcc from emitting pointless destructor code.

Non-local control flow

Another issue that immediately arises when implementing an interpreted language is how commands such as goto, continue, and break are going to work. The basic idea is illustrated in this loop. 

    n = 0; Label["start"]; n = n + 1; If[n < 1000000, Goto["start"]]; Print["done"]
This code start out by setting n to zero, increments it until it gets to a million, then prints "done". This is all done using wonderful Gotos in place of other looping constructs.

The tree representation of this code with which the interpreter works looks like 

    CompoundExpresssion[
      Set[n, 0]
    ,
      Label["start"]
    ,
      Set[
         n
      ,
         Plus[n, 1]
      ]
    ,
      If[
         Less[n, 1000000]
      ,
         Goto["start"]
      ]
    ,
      Print["done"]
    ]
Each node in the tree has builtin code for evaluating it, and the evaluation is applied recursively using the known evaluation rules for Mathematica. For example, when the Goto["start"] is evaluated, this evaluation is called from within the evaluation of the enclosing If, which is itself called from within the CompoundExpression.

Now, the interesting thing is how the Goto["start"] gets back to Label["start"], that is, how the interpreter transfers control to an arbitrary other location. To give an indication of how integrated this control transfer must be with the rest of the system, here is one test from castle's test code (which, of course, is run with On[Assert]). 

    t = Reap[
       i = Pi;
       Block[{i = 1},
           Label["loop"];
           Sow[i];
           MatchQ[i, _ ? (If[# > 5, Sow[i*i]; Goto["out"]]&)];
           i = i + 1;
           Goto["loop"];
       ];
       Assert[False];
       Label["out"];
       i
    ];
    Assert[t === {Pi, {{1, 2, 3, 4, 5, 6, 36}}}];
The Goto["out"] can be called from within the pattern matcher and also can transfer control to a point outside the Block. This is all perfectly legal Mathematica code and expected behaviour. Hence, the Goto["out"] must exit the pattern matcher gracefully and exit the Block gracefully, which involves restoring the value of i from 6 to Pi.

It turns out that we cannot go to truly arbitrary locations in the code. A slight modification of the example above 

    n = 0; If[True, Label["start"]]; n = n + 1; If[n < 1000000, Goto["start"]]; Print["done"]
will result in a failure to find the right label. It turns out that we can only go to labels that are inside compound expressions that enclose, at some level, the corresponding Goto. The label is now inside an If, which renders it invisible to the outer CompoundExpression. Well, this behaviour of Goto screams for an implementation using exceptions.

The implementation of Goto simply throws an object which we hope to catch later: 

    ex dcode_sGoto(er e)
    {
       if (elength(e) != 1)
           return _handle_message_argx1(e);
       throw exception_sym_sGoto(ecopy(e));
       return nullptr;
    }
Now, there are two catchers for exception_sym_sGoto. One is inside the code for CompoudExpression: 
    ex dcode_sCompoundExpression(er e)
    {
       size_t n = elength(e);
       size_t i = 0;
       if (unlikely(n == 0))
           return gs.sym_sNull.copy();
       while (true)
       {
           i++;
           try {
               ex r = eval(ecopychild(e,i));
               if (i < n)
                   eclear(r);
               else
                   return r;
           }
           catch (const exception_sym_sGoto & X)
           {
               uex f(reinterpret_cast(X.data));
               for (i = 1; i <= n; i++)
               {
                   er ei = echild(e,i);
                   if (ehas_head_sym_length(ei, gs.sym_sLabel.get(), 1) &&
                       ex_same(echild(ei,1), f.child(1)))
                   {
                       // have found the correct label, proceed with try block above
                       break;
                   }
               }
               if (i > n)
               {
                   // no label found, search higher up the call stack
                   throw exception_sym_sGoto(f.release());
                   return nullptr;
               }
           }
       }
    }
The other one is at the top level so that an unfound label will gracefully print a message instead of terminating the program as C++ is supposed to do: 
    ex topeval(ex E)
    {
        try
        {
            return eval(E);
        }
        catch (const exception_sym_sGoto & X)
        {
            uex f(reinterpret_cast(X.data));
            _gen_message(gs.sym_sGoto.get(), "nolabel", "Label `1` not found.", f.copychild(1));
            return emake_node(gs.sym_sHold.copy(), f.release());
        }
        ...
    }

C++ exceptions are slow?

We have seen above the following limitations of C++ – that is, the language along with a state-of-the-art compiler in the year 2022:

There is one item that needs to be placed on this list:

The slow down can be seen in action: 

    In[1] := Timing[n = 0; Label["start"]; n = n + 1; If[n < 1000000, Goto["start"]]; Print["done"]]
    "done"
    Out[1] = {3.159714, Null}

    In[2] := Timing[Do[n, {n, 1, 1000000}]]
    Out[2] = {0.016782, Null}

The usual answer to this last point is that exceptions should not be used for control flow, but, in the context of this interpreter, this is precisely what we are doing! Furthermore, considering all of the complicated ways in which Goto is expected to perform, it doesn't seem reasonable to implement it in any other paradigm. Now, the actual implementation of the exceptions can take several forms:

The first option is simply a non-starter with anything at scale (see the interface of LibTomMath for proof). With the second option we get slow gotos but code that is otherwise fast under normal circumstances, and we don't have to deal with return codes at every function call.

asmcastle: Do zero-cost exceptions have to be so slow?

The fundamental operation that exceptions provide is a non-standard way to exit a function call. At the machine level, your function might look like: 

    f:
        construct a local object a
        construct another local object b
        call g
        construct another local object c
        call h
        destruct c
        destruct b
        destruct a
        ret
Now, if g throws (that is, exits in a non-standard way), the exit is supposed to destruct b, then destruct a, then exit f (that is, continue the throw). Similarly, if h throws, c is supposed to be destructed as well. All we need at the machine level is something like: 
    f:
        construct a local object a
        construct another local object b
        call g
        if non-standard exit, goto .unwind1
        construct another local object c
        call h
        if non-standard exit, goto .unwind2
        destruct c
        destruct b
        destruct a
        ret

    .unwind2:
        destruct c

    .unwind1:
        destruct b
        destruct a
        continue non-standard exit
We can do literally anything we like in the unwind code, which includes getting around the uncomfortable fact that C++ destructors are nullary functions.

Anyways, the problem to solve here is how to associate the address of f.unwind1 with the first call to g inside f and similarly for f.unwind2 and h. This is usually done in C++ by keeping some kind of global lookup table in some cold piece of memory. This is certainly possible to do, but the following approach is purely local and a bit more fun: Since the call to g must keep track of the return address somewhere in the machine, we can simply insert a nop after the call to g which encodes f.unwind1. This requires a machine that supports nops with at least a 10-15 bit payload. This is fortunately the case with x86. While inserting a 3, 4, or 7 byte nop after every function call that could throw is not technically zero-cost, it is in some sense zero-cost because a nop literally does nothing.

First, the part of the stack unwinding responsible for looking up the handler: 

    ; zero-cost exceptions, three approaches:
    ;   (1) Have the call site => unwind handler association stored in a global
    ;       table. Maintainance of this global table is tricky, and lookup is slow.
    ;   (2) Include an extra instruction "nop [rax + offset]" at call site in which
    ;       offset = addr(unwind handler) - addr(call site). The unwind_resume
    ;       simply expects a "nop" at the call site and decodes the offset from the
    ;       immediate in the instruction. While this gives a O(1) lookup time for
    ;       call site => unwind handler, it is not technically zero-cost.
    ;         4 byte nop giving 8*4*2^8 = 8*1024 targets:
    ;           zzzzzzzz_01xxx0yy_00011111_00001111
    ;         7 byte nop giving 8*4*2^32 targets:
    ;        .zzzzzzzzzz_10xxx0yy_00011111_00001111
    ;           0yy = 100 is not allowed in either
    ;   (3) 

    ;  in: rax address of exception object
    ;      [rsp] is call site
    unwind_resume:
                pop  rcx                ; rcx = address of call site
               push  rbx rsi rdi
                mov  edx, dword[rcx]    ; disassemble the hopeful nop
                and  edx, 0x00c41f0f
              movzx  esi, byte[rcx + 2]
                and  esi, 0x3b
                cmp  edx, 0x00401f0f
                jne  .not_small_offset
              movsx  rbx, byte[rcx + 3]
    .cont:
                lea  rbx, [rbx + 96]
                shr  esi, 1
                adc  rcx, rsi
                shl  rbx, 5
                shr  esi, 1
                adc  rcx, rbx
                pop  rdi rsi rbx
                jmp  rcx

    .not_small_offset:
                cmp  edx, 0x00801f0f
                jne  .unhandled_exc
             movsxd  rbx, dword[rcx + 3]
                jmp  .cont

    .unhandled_exc:
            ; oops, exit program with unhandled exception
Next, the macro that you are supposed to insert after every call that could throw. There is a 3072 byte shift of the offset because usually the unwind handlers are placed in a later code block, increasing the chances that the nop can fit in 4 bytes instead of 7. 
    macro Unwind a {
        local n, nlo, nmid, nhigh
        n = a - $ - 3072
        nlo = n and 3
        nmid = n and 28
        if n < 0
            nhigh = -1-((-1-n) shr 5)
        else
            nhigh = n shr 5
        end if
        if (-128 <= nhigh) & (nhigh < 128)
            db 0x0f, 0x1f, 64+2*nmid+nlo, nhigh
        else
            db 0x0f, 0x1f, 128+2*nmid+nlo
            dd nhigh
        end if
    }
Finally, the code that you actually have to write to use this. Code that doesn't catch exceptions looks much better, as it just has to pass the exception object onto unwind_resume. 
        ; in: er rax
        ; out: ex rax
    dcode_sCompoundExpression:
               push  rbx rsi rdi
                mov  rbx, rax
                mov  rdi, qword[rax + ex_node.length]
                xor  esi, esi
    .entry:
                cmp  rsi, rdi
                jae  .return_sNull
                jmp  .eval
    .next:
            ExClear  rax
    .eval:
                mov  rax, qword[rbx + ex_node.child + 8*(rsi + 1)]
             ExCopy  rax
               call  ex_eval
             Unwind  .unwind.1
                inc  rsi
                cmp  rsi, rdi
                 jb  .next
    .done:
                pop  rdi rsi rbx
                ret

    .return_sNull:
           ExGetSym  rax, sNull
             ExCopy  rax
                jmp  .done

    .unwind.1:
        ; the call to ex_eval threw: find the type of the exception without
        ; disturbing the actual exception object in rax
                mov  rcx, qword[rax + exc_base.type]
                cmp  rcx, EXC_TYPE_sGoto
                 je  .sGoto
                pop  rdi rsi rbx
                jmp  unwind_resume
    .sGoto:
        ; the exception is a Goto
               push  rbp rax
                mov  rbp, qword[rax + exc_with_ex.data]
                mov  rbp, qword[rbp + ex_node.child + 8*1]
                xor  esi, esi
    .search_next:
                mov  rax, qword[rbx + ex_node.child + 8*(rsi + 1)]
             ExType  edx, rax
           ExGetSym  rcx, sLabel
                cmp  edx, EX_TYPE_NODE
                jne  .not_found
                mov  rdx, qword[rax + ex_node.child + 8*0]
                cmp  qword[rax + ex_node.length], 1
                jne  .not_found
                cmp  rdx, rcx
                jne  .not_found
                mov  rax, qword[rax + ex_node.child + 8*1]
                mov  rcx, rbp
               call  ex_same
             Unwind  .unwind.1.1
               test  eax, eax
                jnz  .found
    .not_found:
        ; rethrow as we didn't find a matching label
                inc  rsi
                cmp  rsi, rdi
                 jb  .search_next
                pop  rax rbp
                pop  rdi rsi rbx
                jmp  unwind_resume
    .found:
        ; free the exception object and continue in the loop
                mov  rbp, qword[rsp]
                mov  rax, qword[rbp + exc_with_ex.data]
            ExClear  rax
                mov  rax, rbp
               call  exc_free
                inc  rsi
                pop  rax rbp
                jmp  .entry

    .unwind.1.1:
        ; exception inside .unwind.1 from ex_same
                mov  rdi, rax
                mov  rbp, qword[rsp]
                mov  rax, qword[rbp + exc_with_ex.data]
            ExClear  rax
                mov  rax, rbp
               call  exc_free
                inc  rsi
                pop  rax rbp
                mov  rax, rdi
                pop  rdi rsi rbx
                jmp  unwind_resume
And the code for generating and throwing the exception from Goto and related functions: 
    dcode_sContinue:
                mov  ecx, EXC_TYPE_sContinue
                jmp  dcode_sReturn.do_it
    dcode_sBreak:
                mov  ecx, EXC_TYPE_sBreak
                jmp  dcode_sReturn.do_it
    dcode_sGoto:
                mov  ecx, EXC_TYPE_sGoto
                jmp  dcode_sReturn.do_it
    dcode_sReturn:
                mov  ecx, EXC_TYPE_sReturn
    .do_it:
               push  rbx rsi rbx
                mov  rbx, rax
                mov  esi, ecx
                mov  eax, sizeof.exc_with_ex
               call  exc_alloc
             ExCopy  rbx
                mov  qword[rax + exc_with_ex.type], rsi
                mov  qword[rax + exc_with_ex.data], rbx
                pop  rdi rsi rbx
                jmp  unwind_resume

Writing code like this is fun at first, but admittedly can get tiresome. As such asmcastle is not very far along: The parser is working and exceptions are used to signal a syntax error, but there is no evaluation nor is there any arithmetic beyond integers.

Pattern matching

Mathematica patterns are essentially regular expressions applied to trees instead of plain old strings. My approach is described here, and this is evidently completely different from WRI's approach.

Expression Compiler

Castle has had a compiler targeting its own internal byte code. This means that the code is still interpreted but that the interpretation is orders of magnitude faster than the main interpreter. Directly targeting x86-64 can give more speed. It is certainly possible to use llvm here, but it is much more fun to emit the machine code oneself. Since the compiler has to do type inference on Mathematica code anyways, much of SSA-based infrastructure for which one would use llvm already must be present.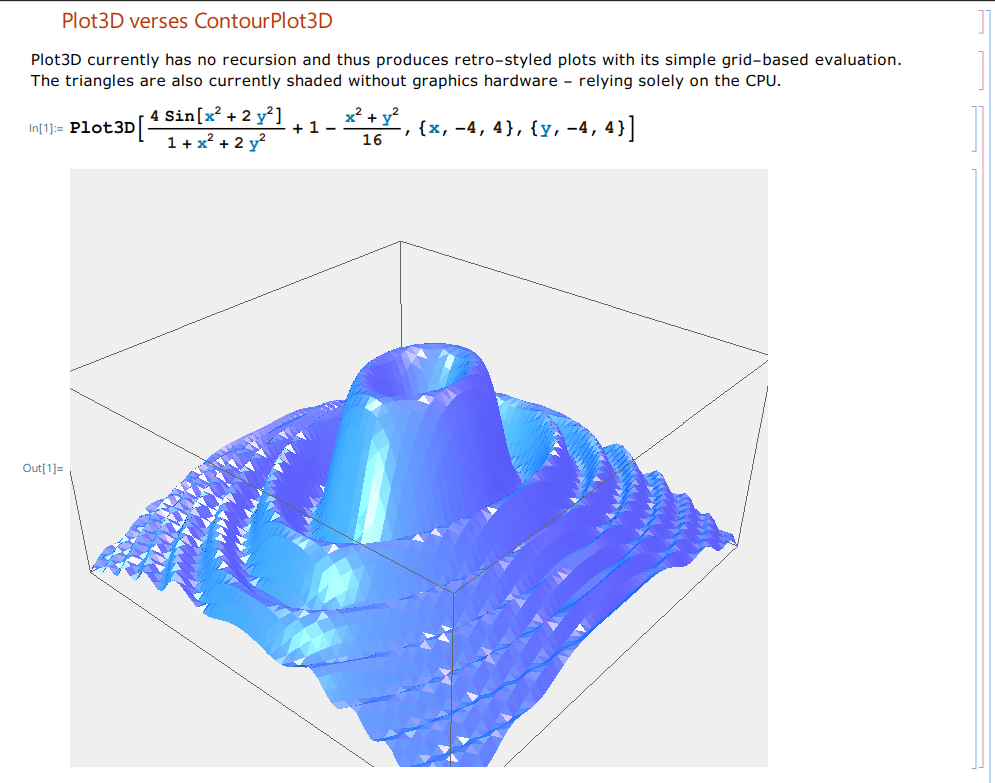 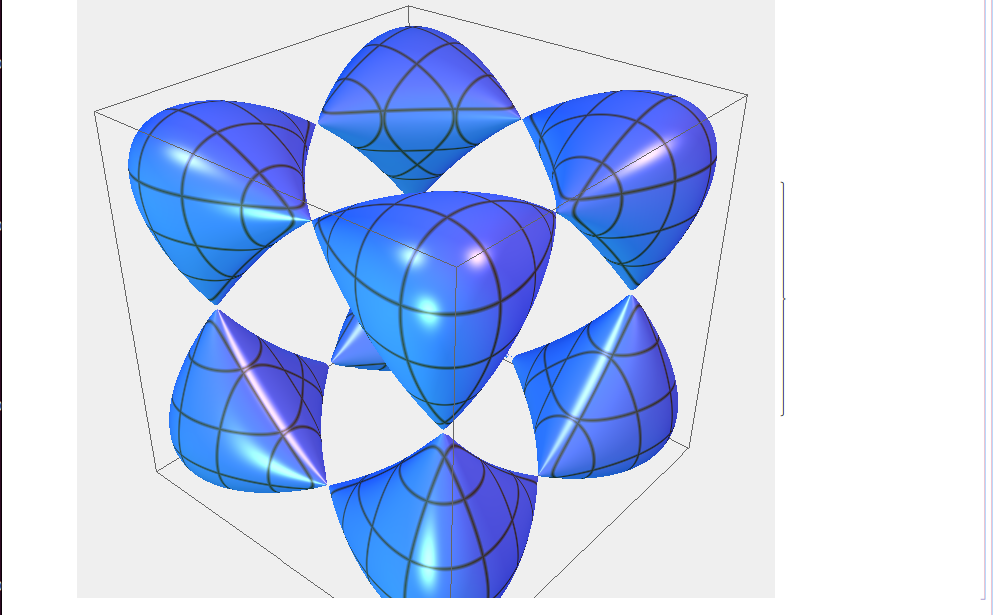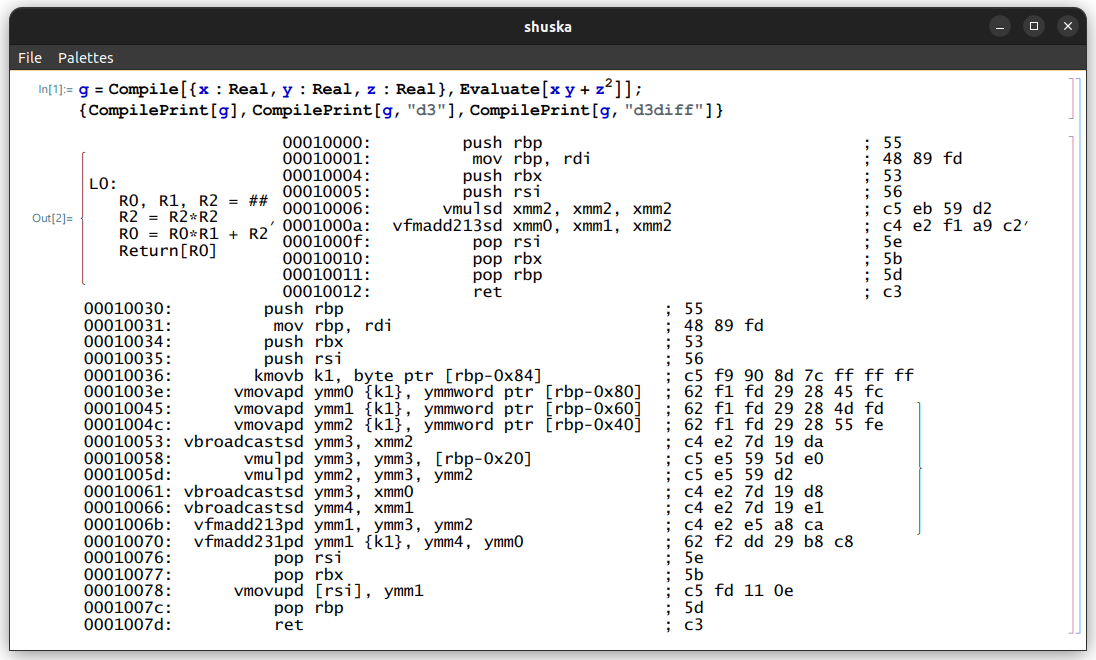Here is a simple example of the internal byte code and two machine code targets. The "d3" and "d3diff" are calling conventions used by the ray tracer to evaluate f(x,y,z) and its gradient. The later is generated from the byte code rather than from the result of symbolic differentiation (D). While this gives slightly larger code than expected in this simple example, it easily scales to loops and other control flow constructs on which D does not operate.

Screenshots

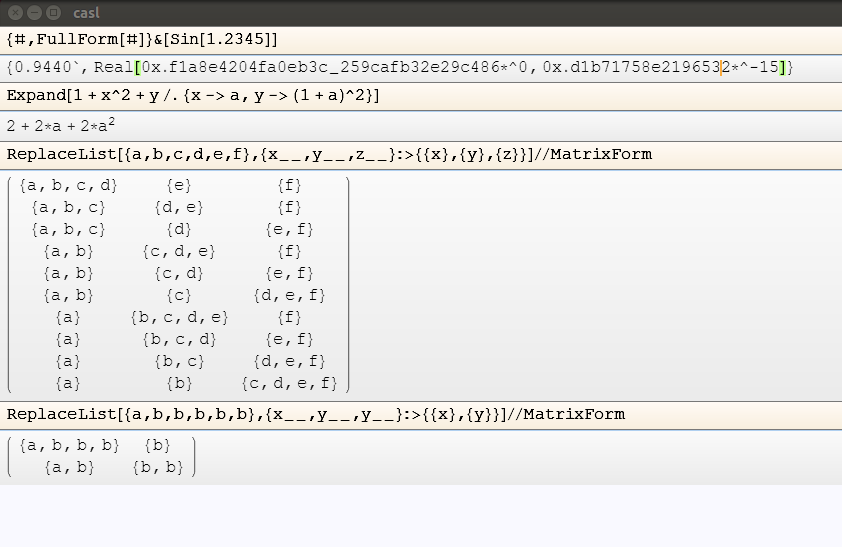
The very first version had poor man's bold and a rather primitive repl compared to the current version. The current version also treats spaces as multiplication, which is a big no-no, but for compatibility what are you going to do.

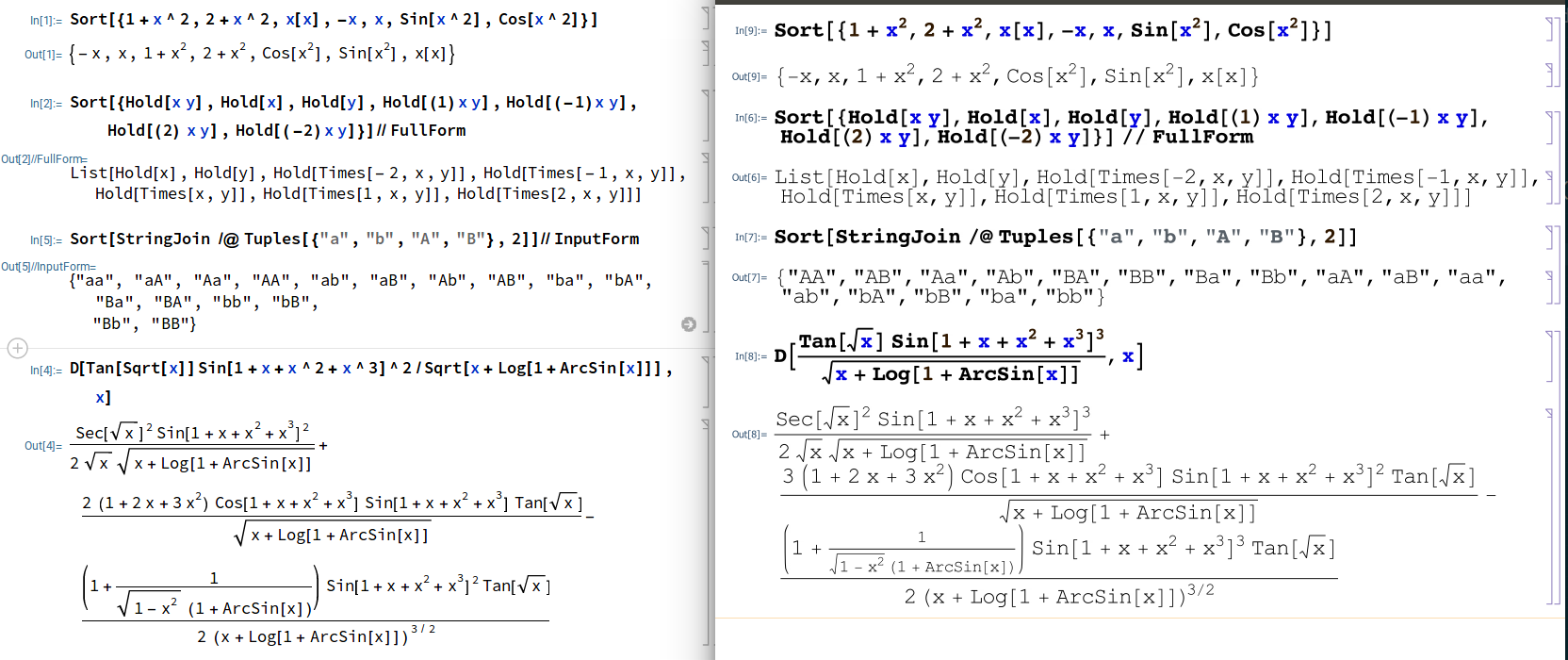
At some point it was pointed out to me that Mathematica orders a sum and a non-sum as if the non-sum was a sum of one term. With this ordering, we seem to match perfectly, though I decided that strings should be compared with std::strcmp.

The syntax highlighting in the GUI is fully recursive as well as the rotation boxes.

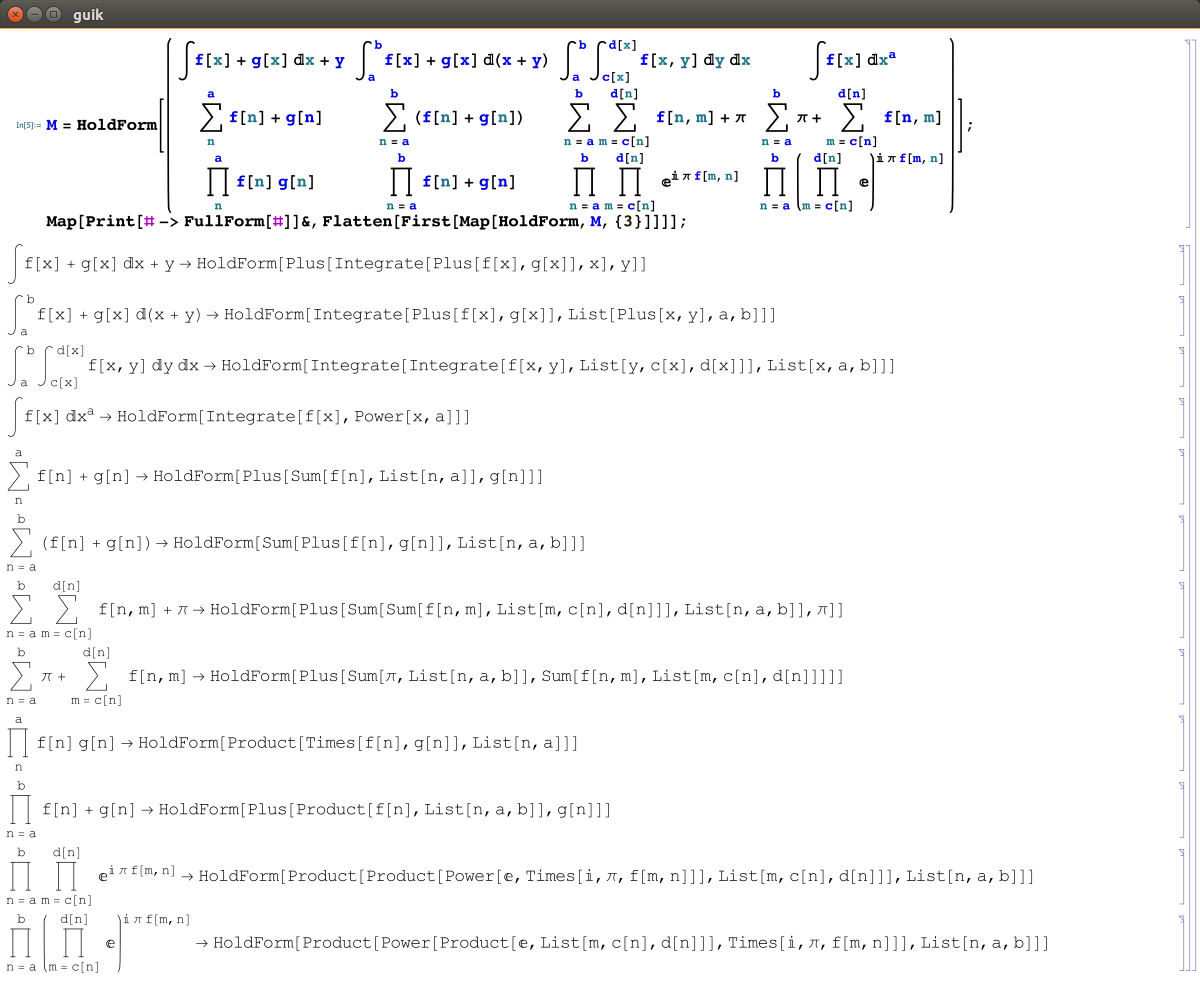
The rotation boxes can be edited in real time, and of course, if the input is upside down, then the output is too.

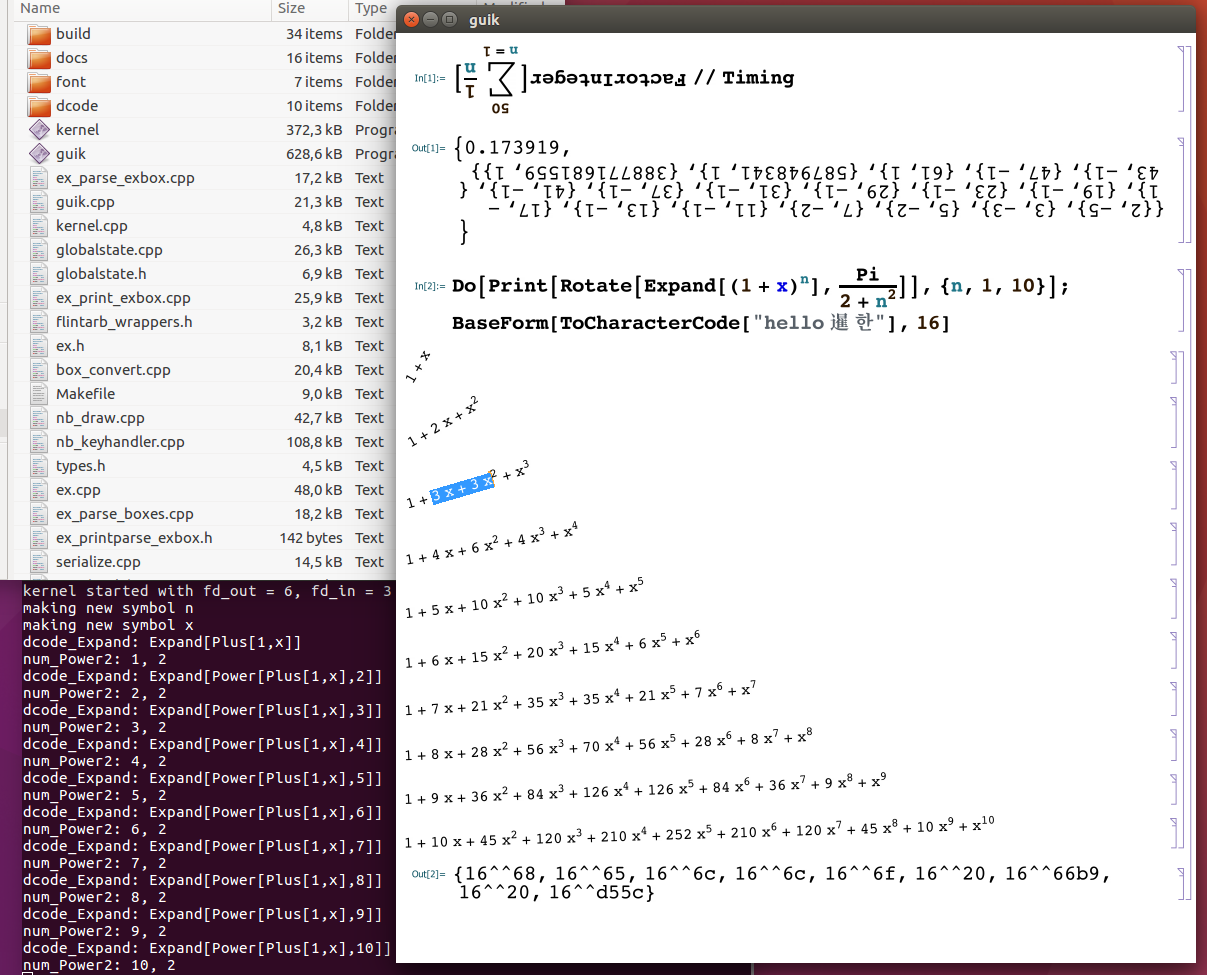
Since pattern matching is at the core of Mathematica, the pattern matcher is one of the first things that must be right.

The font system is completely custom-made and independent from the OS. The only OS-specific code is used for the piping to connect the kernel and GUI, and for the actual display of the bitmap to the screen.